A “linear operator” is just a linear transformation whose domain is the same dimension as its codomain

Score for this quiz: 20 out of 20

Question 1

1 / 1 pts

All identity matrices are symmetric.

Correct!

True

False

Question 2

1 / 1 pts

All upper-triangular matrices are symmetric.

True

Correct!

False

Question 3

1 / 1 pts

All square matrices have the same number of rows as columns.

Correct!

True

False

Question 4

1 / 1 pts

A “linear operator” is just a linear transformation whose domain is the same dimension as its codomain (for example, it maps each vector in ℛ⁵ to another vector in ℛ⁵.)

Correct Answer

True

You Answered

False

Question 5

1 / 1 pts

If I perform a linear transformation on a 2-dimensional vector x by multiplying it on the left by the matrix A below (i.e., performing the multiplication Ax) the vector will be rotated 90 degrees clockwise.

$\left[\begin{array}{cc} 0&1 \\ -1&0 \\ \end{array}\right]$

Correct Answer

True

You Answered

False

Question 6

2 / 2 pts

Let y be the vector that the linear transformation $\begin{bmatrix} 2 & 1 & -3 \\ 4 & 1 & 1 \end{bmatrix}$ maps the vector $\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}$ to. Which of the following is true of y? Check all that apply.

Correct!

all of its elements are even

you can’t even do that operation

it is 3 dimensional

one of its elements is -3

Correct!

it is 2 dimensional

it has all zeros

it is 9 dimensional

it is 6 dimensional

Question 7

1 / 1 pts

What’s the rank of the following matrix?

Correct!

Correct Answers

2.0 (with margin: 0.0)

Question 8

0 / 1 pts

What’s the rank of the following matrix?

$\left[\begin{array}{ccc} 4&0&1 \\ 3&-4&3 \\ 1&4&-2\end{array}\right]$

You Answered

Correct Answers

2.0 (with margin: 0.0)

Question 9

2 / 2 pts

Which of the following is true of the matrix operation below? (Check all that apply)

the operation can’t be done

Correct!

all its entries are non-zero

Correct!

it is a 2×2 matrix

it is a scalar

all its entries are even

it is a 1×2 vector

Correct!

all its entries are positive

it is a 2×1 vector

Question 10

2 / 2 pts

Which of the following is true of the result of the matrix-vector multiplication below? (check all that apply)

Correct!

all of its entries are positive

it is a scalar

Correct!

one of its entries is 16

this operation can’t be done

it is a 3×3 matrix

all of its entries are even

it is a 1×1 matrix

Question 11

1 / 1 pts

If two matrices M and N are the same dimensions (i.e., M and N each have the same number of rows, and also M and N each have the same number of columns), then you can definitely add them together.

Correct!

True

False

Question 12

1 / 1 pts

If a matrix Q has 13 rows, and p is a vector with 13 elements, you can definitely multiply Q times p.

True

Correct!

False

Question 13

1 / 1 pts

The vector $\begin{bmatrix} 3 \\ 2 \end{bmatrix}$ is in the kernel of the matrix $\begin{bmatrix} -4 & 6 \\ 2 & -3 \end{bmatrix}$ .

Correct!

True

False

Question 14

1 / 1 pts

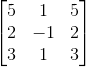The vector $\begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}$ is in the kernel of the matrix $\begin{bmatrix} 5 & 1 & 5 \\ 2 & -1 & 2 \\ 3 & 1 & 3 \end{bmatrix}$ .